Learning Cases and Strategies
Across different schools and systems, I have always been drawn to concrete learning cases: how real classrooms embody inquiry, collaboration, technology, and student agency. The following examples, together with my own practices, have shaped how I think about mathematics education and interdisciplinary design.
Learning Cases: Inquiry, Collaboration, and Technology
Inquiry-based learning is emphasized: students engage in mathematics research projects where they share their goals, challenges, and expectations, fostering their research and communication skills through peer interaction. Collaborative learning is another highlight: students work together on problem-solving exercises, supporting one another and enhancing their teamwork and collective learning abilities. The integration of technology is also central: tools such as wiki pages serve as communication and learning resources, enhancing students’ digital literacy.
- Student-centered teaching methodology: The teacher prioritizes providing students with opportunities to express their ideas, fostering independent learning.
- Focus on real-world application: Through research projects and practice with real exam questions, students gain a deeper understanding of how mathematics applies to real life.
- Development of diverse skills: Beyond mathematical knowledge, the course emphasizes communication, research, and technology application, cultivating interdisciplinary competencies.
- Encouraging active participation: By allowing voluntary presentations and promoting teamwork, students gain confidence through meaningful engagement.
Interdisciplinary Calculus & String Art: The Bombay International School Case
At Bombay International School, the Collaborative Mathematics and Art Unit on Calculus and String Art offers an innovative and interdisciplinary approach:
- Integration of ATL skills: Communication, critical thinking, and self-management skills are embedded into the mathematics curriculum, fostering holistic student development.
- Student-led learning: Students are encouraged to discuss, collaborate, and reflect, nurturing their autonomy and ownership of their learning journey.
- Application to real-life contexts: The unit ties abstract and challenging mathematical concepts with visually captivating and tangible art, helping students understand the practical beauty of mathematics.
By combining abstract mathematical ideas with intuitive and aesthetic art, this kind of program unveils the beauty of mathematics in everyday life.
It connects math to art and everyday experience, making learning both practical and inspirational. Such an approach not only enriches students’ understanding of mathematics and art but also fosters a deeper appreciation of the interconnectedness of disciplines, creativity, and the world around them.
Personal Reflection: My Own Learning Designs
I believe I have successfully implemented several effective strategies in my teaching. I have actively sought to integrate mathematics within other disciplines within the school, aiming to stimulate students’ enthusiasm for the subject and help them discover and experience the inherent beauty of mathematics. For example, I organized a three-dimensional Sudoku activity in the international department, where I combined less engaging mathematical concepts with broader, exploratory challenges. This approach encouraged students to engage more actively with mathematics, as it transformed abstract ideas into something tangible and enjoyable.
Furthermore, I have experimented with innovative ways to present mathematical ideas. One such initiative was creating mathematical magazines. These visual and accessible publications used fun, simple, and intuitive formats to unravel the mysteries of mathematics. This allowed students to explore complex concepts in a way that felt less intimidating and more engaging, fostering a sense of curiosity and appreciation for the subject.
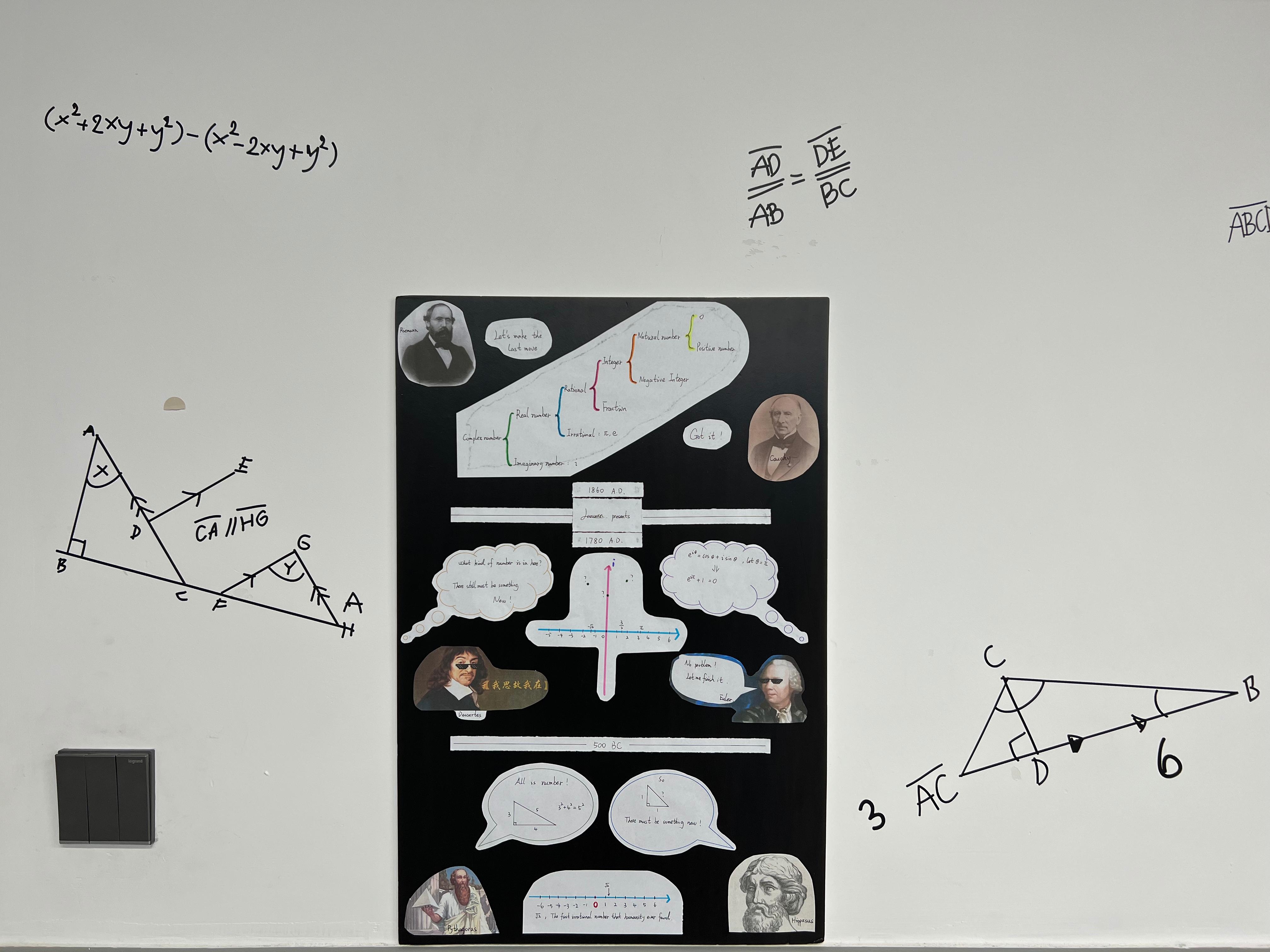
A poster from my mathematical magazine project, where abstract ideas were turned into visual stories for students.
Areas for Growth and Future Directions
However, reflecting on my practices, I recognize areas where I can improve to achieve greater impact:
- Integrating local and international perspectives: While I strive to make mathematics engaging, I realize the importance of aligning my teaching more closely with the local cultural framework while incorporating international learning methodologies. This could help students see the relevance of mathematical ideas in their immediate cultural context while preparing them for a global academic environment.
- Enhancing coherence in mathematical understanding: A significant area for growth lies in strengthening the continuity and coherence of the subject. It is crucial to ensure that students not only understand individual concepts but also grasp how these ideas connect across topics and levels, so that they can approach problems with a more integrated perspective.
- Fostering deeper exploration: While activities like Sudoku and mathematical magazines generate interest, I need to explore methods to encourage students to delve deeper into mathematical reasoning and problem-solving—similar to the case at Bombay International School, where students apply mathematics to real life through a useful framework.
- Feedback and reflection: Another aspect I can enhance is creating a systematic feedback loop for both myself and my students. Regular reflection sessions could help students articulate what they’ve learned and identify areas for improvement, while also providing me with valuable insights to refine my teaching methods.
- Professional development: To stay aligned with best practices, I should continue seeking opportunities to learn from international and local educators. This could involve workshops, collaborative teaching projects, or participating in interdisciplinary educational programs.
Ultimately, these learning cases and strategies remind me that good mathematics teaching is not only about content coverage, but about designing experiences that connect curiosity, culture, and deeper understanding.